סטטיסטיקה היא אחת הדרכים להציג את ההיסטוריה של העסק. תוצאת הסטטיסטיקה כבר אינה סטטיסטיקה. אלא מערכת נתונים המיועדת לכוון להחלטות שיווקיות או במילים אחרות להוביל לרווחים גדולים יותר (הגדרנו כבר את השיווק כהנדסת הרווחים של העסק!). הבעיה מסתבכת כאשר המציאות שונה מהתחזיות, ואז צריכים לבדוק מה קרה: המציאות השתנתה או המדידה לא הייתה מדויקת. וכמעט תמיד נגלה כי לא הייתה התייחסות לכל הנתונים, וגם שההתייחסות לא הייתה מדויקת ולכן התחזית לא ניתחה עוד מצבים אפשריים. כאן יש לשאול

מספר שאלות לפני שמתחילים עם איסוף הנתונים (וזה הרבה לפני הניתוח):

א. מה נרצה לעשות עם התוצאות.
ב. מה נמדוד לצורך זה.
ג. מה תהיה ההוכחה שמדדנו נכון.

מתי מגיעים לשום מקום? בשני מיקרים:

1. כשמנתחים מספרים לא נכונים.
2. כשמנתחים לא נכון מספרים נכונים.

כללית סטטיסטיקה מבוססת על 6 רבדים:

1. האוכלוסייה עצמה (כמותית. ה 100%).
2. איסוף הנתונים: בדיקה.דגימה או כולה.
3. עיבוד ישיר של המספרים (סדרה, התפלגות, ממוצע, שכיח, חציון, עשירון וכו').
4. היחסים בין הנתונים (שונות, מתאם).
5. אימות הנתונים (מהימנות, מובהקות ותוקף).
6. תחזית, חיזוי והכללה.

המלצה: תחילת המעשה בסוף המחשבה©

1. האוכלוסיה עצמה: מספרים הם בסיס לשפה. בדיוק כמו אותיות. נוסחאות הם משפטים באותה שפה, שבה כותבים מספרים.

כמו אותיות, כשמספרים מצטרפים אחד לשני מקבלים מילה. ולאלו יש משמעויות שונות. תלוי בהקשר בו הן מופיעות. בפרק זה נבדוק אם לכל מספר (ובייחוד לאפס) יש אותה משמעות בצירופים שונים. להלן סוגי מספרים/סולמות שונים: מספר זיהוי/סולם שמי. מספר סידורי/סולם פשוט. מספר איכות/סולם מרווח. מספר רציונאלי/סולם כמותי/או מנה. טעות בהבנת התוצאות נוצרת מהנחות יסוד שגויות לגבי מהות המספרים וזיהוי הסולם על פיו בוצעה המדידה. לגבי הנחות לא מאומתות נא לזכור את משפט ההדגמה הבא:

.Never assume because you make an ass of u and me

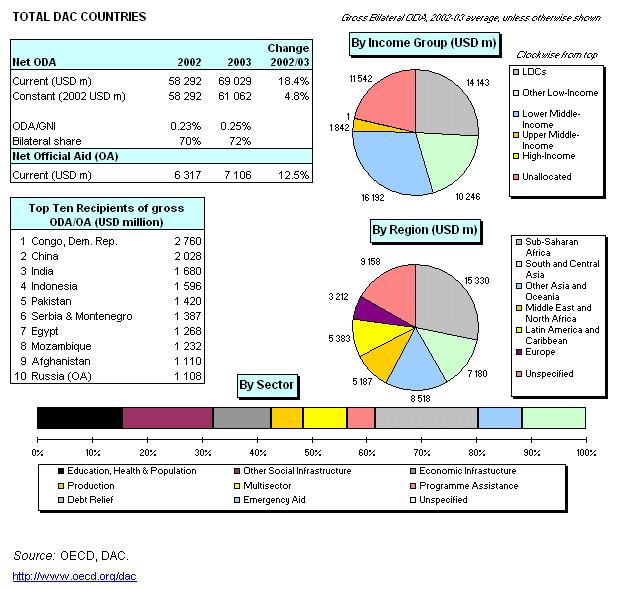
2. עיבודים סטטיסטיים: כדי להדגים ניקח כדוגמה את שאלת השכר. מה לומדים מהדו"ח הסטטיסטי? שהשכר הממוצע נמצא

בין העשירון השלישי לרביעי. שהשכיח נמצא בעשירון השלישי. ושהשכר החציוני נמצא בעשירון השמיני. (תרגום קצר: 2/3 האוכלוסייה מקבל 1/3 מההכנסות) זה בא להדגים מה קורה כשמתייחסים לממוצע בלבד ומתעלמים מנתונים אחרים במסגרת אותה המדידה, וכך מאבדים את המשמעות האמיתית של התוצאות .

3. התנהגות המספרים:

מתאם ושונות. זה שורש של זו. זו תחילת הבעייתיות כשאין זיהוי נכון של הסולמות, משום שנדרשת שיטת ניתוח שונה מסולם לסולם. ולא תמיד משקיעים, בבדיקה מראש של המשתנים הנמדדים על מנת לוודא איזה סוג של סולמות/מספרים הם. וכך מגיעים למסקנות לא נכונות, בייחוד כשיש השפעות גומלין בין נתונים שונים באותו מדגם (משתנים מתווכים)

4. אימות הנתונים:

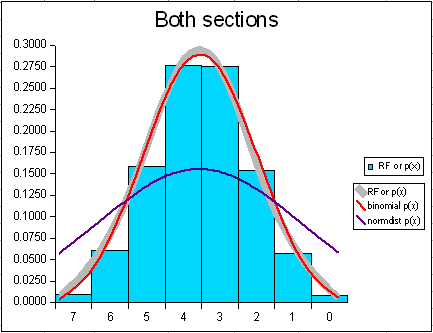
מהימנות, מובהקות ותקפות, מי מבחין מי יודע? זה בעצם אומר מה מדדנו. למשל מה מייצג ומה לא. ועל מה ניתן לסמוך ועד כמה. ואיך נדע ש"מדגם מייצג" זה לא אטריות? מדידה חוזרת אמורה לענות על הדברים: שאלות זהות בניסוח שונה. דגימה חוזרת או חלוקת המדגם. השוואה להתפלגות נורמלית או סטטיסטית אחרת. וגם, בדיקה רעיונית.

5. איסוף הנתונים:

דגימה: מדגם מקרי מייצג זה טעון כוזב (fallacy). מדגם מקרי אינו יכול לייצג. גם לא במקרה! כי על מנת להגיע ל"ייצוג" יש צורך לדאוג שכל המשתנים יהיו "מיוצגים" ולזה אי אפשר להגיע ב"מקרה"! לכן על מנת לוודא ייצוג, על המדגם להיות מתוכנן.בין בשכבות או באשכולות. ומכאן שאם המדגם מקרי - מייצג הוא לא! מדגם מתוכנן, הוא גם הרבה יותר יעיל משום שאפשר לבנותו כך, שידאג לייצוג כל האוכלוסיות ותת אוכלוסיות שאת התנהגותן מבקשים למדוד.

6. תחזית חיזוי והכללות:

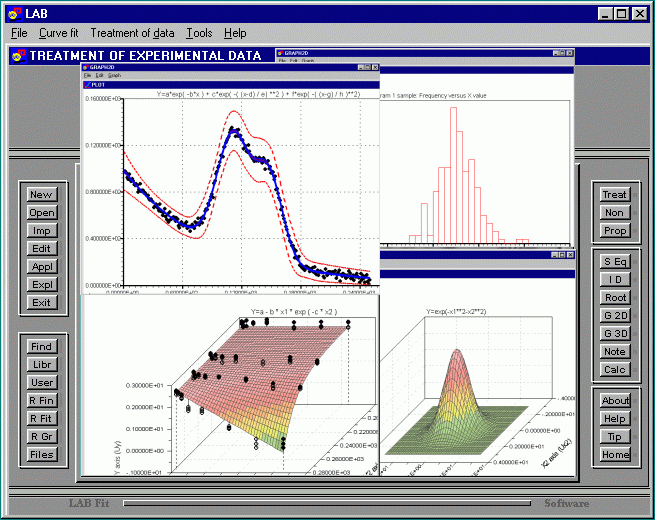
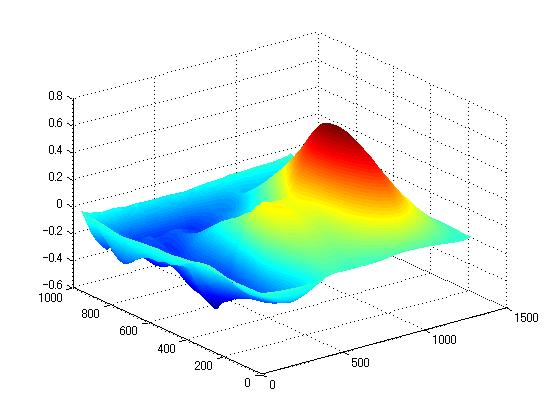
התוצאה המתבקשת מכל ניתוח סטטיסטי, שאינו לצורכי היסטוריה. והרבה פעמים הבדיחה העיקרית בתוצאות העבודה. בפרק זה נבחן כאן מהם תנאי הסף לחיזוי. כיצד תיראה התחזית. למה המציאו CFA ו EFA ומתי לא צריך הכללות. הגישה הטכנית (לפעמים בבורסה) נשענת בדרך כלל על סדרות זמן, הגם שאינה מכנה אותן כך. מאידך יש לזכור כי בכל נקודת זמן שבה משתמשים בממוצעים, אלו מיצגים התפלגות שאינה נראית בהכרח כמו ריצת התוצאות ולכן מומלץ, על מנת להקטין את שיעור הטעות (מקרית או קבועה ייבדק בנפרד) – לבצע ניתוח תלת ממדי של התנהגות הנתונים.

ואם לא ברור בדיוק מה תיארנו עד כאן. תישאלו אותנו. נשמח להסביר!

איך עושים מחקר שוק בלי אטריות – תקציר הספור השלם:

מחקר מתחיל תמיד מהשאלה א. מה נרצה לעשות עם התוצאות. במילים אחרות, בשביל מה צריך את זה. גם אם זה רק בשביל לדעת, צריך להחליט מראש כמה מדויק המחקר צריך להיות. ואז לשאול:
ב. מה נמדוד לצורך זה. לפני שדוגמים. כאן נגדיר מה דוגמים. את השאלות שנשאל ומה התשובות שאנו מצפים לקבל (H?). ואיזה סוג נתונים אנו צופים לקבל ומדוע. ועל בסיס הגדרה זו - מה תהיה שיטת הניתוח, מבנה המחקר, גודל המדגם, תקציבו ומי יהיה אחראי לעבודה.
ג. בכל שיטה/שיטות שנבחר, מה יהיה בסיס ההוכחה שמדדנו נכון. וזה חשוב כדי לדעת עד כמה ניתן יהיה לסמוך על התוצאות. חשוב שבעתיים כשמסתמכים על הנתונים לצורך הכנת תחזית.